Surface Areas and Volumes
CHAPTER 13
Surface Areas and Volumes
Surface Area and Volumes Formulas
Surface Areas and Volumes of Solids
(i) Cuboid:
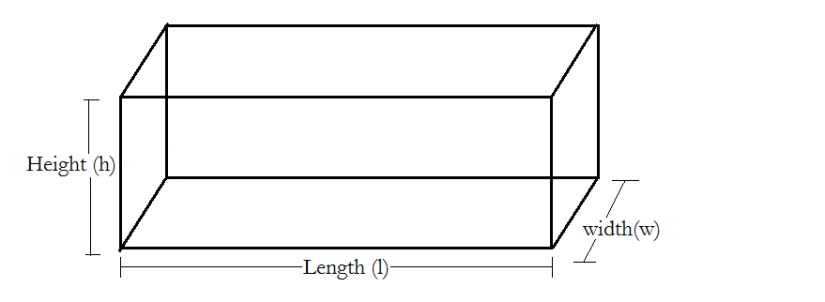
Volume = l × b × h
Total surface area = 2 [lb + bh + hl]
Lateral surface area = 2 [bh + hl]
Diagonal of the coboid =
(ii) Cube:
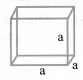
Volume = a3
Total surface area = 6a2
Lateral surface area = 4a2
Diagonal of a cube = √3a
(iii) Cylinder:
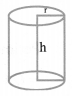
(a) Right circular cylinder:
Volume = πr2h
Curved Surface Area = 2nrh
Total Surface Area= 2πrh + 2πr2 = 2πr(r + h)
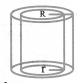
(b) Right circular hollow cylinder:
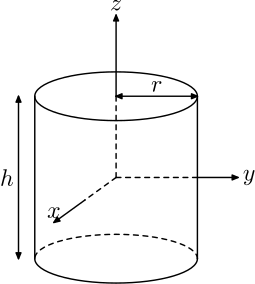
Let r and R be internal & external radii.
Volume = n(R2 – r2)h
Curved Surface Area = 2π(R + r)h
Total Surface Area = 2π(R + r)h + 2π(R2 – r2)
= 2π(R + r)(h + R — r)
(iv) Right circular cone:
Slant height, l = 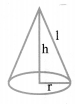
Volume =
Curved Surface Area = πrl
Total Surface Area = πrl + πr2
Surface Areas and Volumes of Sphere and Hemisphere
(i) Sphere:
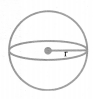
Volume =
Surface area =4πr2
(ii) Hemisphere:

Volume =
C.S.A = 2πr2
T.S.A = 3πr2
(iii) Hemispherical shell:
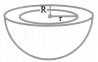
Volume =
Curved Surface Area = 2π(R2 + r2)
Total Surface Area = 2π(r2 + R2) + n (R2 – r2)
= π (r2 + 3R2)
Surface Areas of a Combination of Solids
The surface area of a solid which is a combination of two or more solids is calculated by adding the surface areas of the individual solids which are visible in the new solid formed.
For Example:
If we consider the surface of the newly formed object as given in the figure above, we would be able to see only the curved surfaces of the two hemispheres and the curved surface of the cylinder.
So, the total surface area of the new solid is the sum of the curved surface areas of each of the individual parts. This gives, TSA of new solid = CSA of one hemisphere + CSA of cylinder + CSA of other hemisphere
Volume of a Combination of Solids
Whenever solid is formed by combining two or more solids, then the amount of matter present in the new solid is equal to the sum of amounts of matter in the constituting solids. Volume of new solid = sum of the volumes of the individual solids
Conversion of Solid form One Shape to Another
(i) When a solid is converted from one shape to other, then its volume remains same only its shape and size changes.
(ii) If a solid is converted into a number of small identical solids, then Number of small items
Frustum of a Cone [Very Important for Board Exam]
When we slice (or cut) through a cone with a plane parallel to its base (see below figure ) and remove the cone that is formed on one side of that plane, the part that is now left over on the other side of the plane is called a frustum of the cone.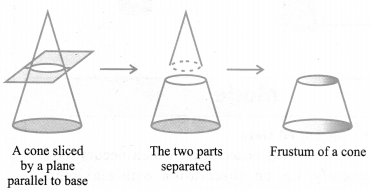
(i) Volume of the frustum of cone
(ii) C.S.A. of the frustum of cone = π(r1 + r2)l,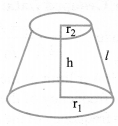
where l =
(iii) T.S.A. of the frustum of cone
l =
- Sphere Formulas
Diameter of sphere 2r Surface area of sphere 4 π r2 Volume of Sphere 4/3 π r3
- Cylinder Formulas
Curved surface area of Cylinder 2 πrh Area of two circular bases 2 πr2 Total surface area of Cylinder Circumference of Cylinder + Curved surface area of Cylinder = 2 πrh + 2 πr2 Volume of Cylinder π r2 h
- Cone Formulas
Slant height of cone l = √(r2 + h2) Curved surface area of cone πrl Total surface area of cone πr (l + r) Volume of cone ⅓ π r2 h
- Cuboid Formulas
Perimeter of cuboid 4(l + b +h) Length of the longest diagonal of a cuboid √(l2 + b2 + h2) Total surface area of cuboid 2(l×b + b×h + l×h) Volume of Cuboid l × b × h
| Diameter of sphere | 2r |
| Surface area of sphere | 4 π r2 |
| Volume of Sphere | 4/3 π r3 |
| Curved surface area of Cylinder | 2 πrh |
| Area of two circular bases | 2 πr2 |
| Total surface area of Cylinder | Circumference of Cylinder + Curved surface area of Cylinder = 2 πrh + 2 πr2 |
| Volume of Cylinder | π r2 h |
| Slant height of cone | l = √(r2 + h2) |
| Curved surface area of cone | πrl |
| Total surface area of cone | πr (l + r) |
| Volume of cone | ⅓ π r2 h |
| Perimeter of cuboid | 4(l + b +h) |
| Length of the longest diagonal of a cuboid | √(l2 + b2 + h2) |
| Total surface area of cuboid | 2(l×b + b×h + l×h) |
| Volume of Cuboid | l × b × h |
Here, l = length, b = breadth and h = height In case of Cube, put l = b = h = a, as cube all its sides of equal length, to find the surface area and volumes.
Exercise 13.1
1. 2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Answer:
The diagram is given as:

Given,
The Volume (V) of each cube is = 64 cm3
This implies that a3 = 64 cm3
∴ a = 4 cm
Now, the side of the cube = a = 4 cm
Also, the length and breadth of the resulting cuboid will be 4 cm each. While its height will be 8 cm.
So, the surface area of the cuboid = 2(lb+bh+lh)
= 2(8×4+4×4+4×8) cm2
= 2(32+16+32) cm2
= (2×80) cm2 = 160 cm2
2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Answer:
The diagram is as follows:

Now, the given parameters are:
The diameter of the hemisphere = D = 14 cm
The radius of the hemisphere = r = 7 cm
Also, the height of the cylinder = h = (13-7) = 6 cm
And, the radius of the hollow hemisphere = 7 cm
Now, the inner surface area of the vessel = CSA of the cylindrical part + CSA of hemispherical part
(2πrh+2πr2) cm2 = 2πr(h+r) cm2
2×(22/7)×7(6+7) cm2 = 572 cm2
3. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Answer:
The diagram is as follows:

Given that the radius of the cone and the hemisphere (r) = 3.5 cm or 7/2 cm
The total height of the toy is given as 15.5 cm.
So, the height of the cone (h) = 15.5-3.5 = 12 cm

∴ The curved surface area of cone = πrl
(22/7)×(7/2)×(25/2) = 275/2 cm2
Also, the curved surface area of the hemisphere = 2πr2
2×(22/7)×(7/2)2
= 77 cm2
Now, the Total surface area of the toy = CSA of cone + CSA of hemisphere
= (275/2)+77 cm2
= (275+154)/2 cm2
= 429/2 cm2 = 214.5cm2
So, the total surface area (TSA) of the toy is 214.5cm2
4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Answer:
It is given that each side of cube is 7 cm. So, the radius will be 7/2 cm.

We know,
The total surface area of solid (TSA) = surface area of cubical block + CSA of hemisphere – Area of base of hemisphere
∴ TSA of solid = 6×(side)2+2πr2-πr2
= 6×(side)2+πr2
= 6×(7)2+(22/7)×(7/2)×(7/2)
= (6×49)+(77/2)
= 294+38.5 = 332.5 cm2
So, the surface area of the solid is 332.5 cm2
5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Answer:
The diagram is as follows:

Now, the diameter of hemisphere = Edge of the cube = l
So, the radius of hemisphere = l/2
∴ The total surface area of solid = surface area of cube + CSA of hemisphere – Area of base of hemisphere
TSA of remaining solid = 6 (edge)2+2πr2-πr2
= 6l2 πr2
= 6l2+π(l/2)2
= 6l2+πl2/4
= l2/4(24+π) sq. units
6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

Answer:
Two hemisphere and one cylinder are shown in the figure given below.

Here, the diameter of the capsule = 5 mm
∴ Radius = 5/2 = 2.5 mm
Now, the length of the capsule = 14 mm
So, the length of the cylinder = 14-(2.5+2.5) = 9 mm
∴ The surface area of a hemisphere = 2πr2 = 2×(22/7)×2.5×2.5
= 275/7 mm2
Now, the surface area of the cylinder = 2πrh
= 2×(22/7)×2.5×9
(22/7)×45 = 990/7 mm2
Thus, the required surface area of medicine capsule will be
= 2×surface area of hemisphere + surface area of the cylinder
= (2×275/7) × 990/7
(550/7) + (990/7) = 1540/7 = 220 mm2
7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of Rs 500 per m2. (Note that the base of the tent will not be covered with canvas.)
Answer:
It is known that a tent is a combination of cylinder and a cone.

From the question we know that
Diameter = 4 m
Slant height of the cone (l) = 2.8 m
Radius of the cone (r) = Radius of cylinder = 4/2 = 2 m
Height of the cylinder (h) = 2.1 m
So, the required surface area of tent = surface area of cone + surface area of cylinder
= πrl+2πrh
= πr(l+2h)
= (22/7)×2(2.8+2×2.1)
= (44/7)(2.8+4.2)
= (44/7)×7 = 44 m2
∴ The cost of the canvas of the tent at the rate of ₹500 per m2 will be
= Surface area × cost per m2
44×500 = ₹22000
So, Rs. 22000 will be the total cost of the canvas.
8. From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the
same height and same diameter is hollowed out. Find the total surface area of the
remaining solid to the nearest cm2.
Answer:
The diagram for the question is as follows:

From the question we know the following:
The diameter of the cylinder = diameter of conical cavity = 1.4 cm
So, the radius of the cylinder = radius of the conical cavity = 1.4/2 = 0.7
Also, the height of the cylinder = height of the conical cavity = 2.4 cm

Now, the TSA of remaining solid = surface area of conical cavity + TSA of the cylinder
= πrl+(2πrh+πr2)
= πr(l+2h+r)
= (22/7)× 0.7(2.5+4.8+0.7)
= 2.2×8 = 17.6 cm2
So, the total surface area of the remaining solid is 17.6 cm2
Question 9.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in figure. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
Solution: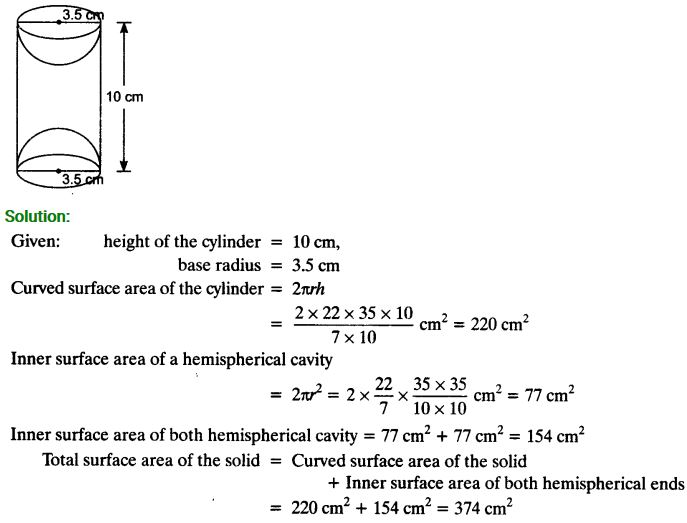
Exercise: 13.2
(Page No: 247)
1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Solution:
Here r = 1 cm and h = 1 cm.
The diagram is as follows.

Now, Volume of solid = Volume of conical part + Volume of hemispherical part
We know the volume of cone = ⅓ πr2h
And,
The volume of hemisphere = ⅔πr3
So, volume of solid will be

= π cm3
2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminum sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Solution:
Given,
Height of cylinder = 12–4 = 8 cm
Radius = 1.5 cm
Height of cone = 2 cm
Now, the total volume of the air contained will be = Volume of cylinder+2×(Volume of cone)
∴ Total volume = πr2h+[2×(⅓ πr2h )]
= 18 π+2(1.5 π)
= 66 cm3.
3. A Gulab jamun contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 Gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see figure).

Solution:
It is known that the gulab jamuns are similar to a cylinder with two hemispherical ends.
So, the total height of a gulab jamun = 5 cm.
Diameter = 2.8 cm
So, radius = 1.4 cm
∴ The height of the cylindrical part = 5 cm–(1.4+1.4) cm
=2.2 cm
Now, total volume of One Gulab Jamun = Volume of Cylinder + Volume of two hemispheres
= πr2h+(4/3)πr3
= 4.312π+(10.976/3) π
= 25.05 cm3
We know that the volume of sugar syrup = 30% of total volume
So, volume of sugar syrup in 45 gulab jamuns = 45×30%(25.05 cm3)
= 45×7.515 = 338.184 cm3
4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig.).

Solution:
Volume of cuboid = length x width x height
We know the cuboid’s dimensions as 15 cmx10 cmx3.5 cm
So, the volume of the cuboid = 15x10x3.5 = 525 cm3
Here, depressions are like cones and we know,
Volume of cone = (⅓)πr2h
Given, radius (r) = 0.5 cm and depth (h) = 1.4 cm
∴ Volume of 4 cones = 4x(⅓)πr2h
= 1.46 cm2
Now, volume of wood = Volume of cuboid – 4 x volume of cone
= 525-1.46 = 523.54 cm2
5. A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Solution:
For the cone,
Radius = 5 cm,
Height = 8 cm
Also,
Radius of sphere = 0.5 cm
The diagram will be like

It is known that,
Volume of cone = volume of water in the cone
= ⅓πr2h = (200/3)π cm3
Now,
Total volume of water overflown= (¼)×(200/3) π =(50/3)π
Volume of lead shot
= (4/3)πr3
= (1/6) π
Now,
The number of lead shots = Total Volume of Water over flown/ Volume of Lead shot
= (50/3)π/(⅙)π
= (50/3)×6 = 100
6. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8 g mass.
Solution:
Given, the height of the big cylinder (H) = 220 cm
Radius of the base (R) = 24/12 = 12 cm
So, the volume of the big cylinder = πR2H
= π(12)2 × 220 cm3
= 99565.8 cm3
Now, the height of smaller cylinder (h) = 60 cm
Radius of the base (r) = 8 cm
So, the volume of the smaller cylinder = πr2h
= π(8)2×60 cm3
= 12068.5 cm3
∴ Volume of iron = Volume of the big cylinder+ Volume of the small cylinder
= 99565.8 + 12068.5
=111634.5 cm3
We know,
Mass = Density x volume
So, mass of the pole = 8×111634.5
= 893 Kg (approx.)
7. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Solution:

Here, the volume of water left will be = Volume of cylinder – Volume of solid
Given,
Radius of cone = 60 cm,
Height of cone = 120 cm
Radius of cylinder = 60 cm
Height of cylinder = 180 cm
Radius of hemisphere = 60 cm
Now,
Total volume of solid = Volume of Cone + Volume of hemisphere
Volume of cone = π×122×103cm3 = 144×103π cm3
So, Total volume of solid = 144×103π cm3 -(⅔)×π×103 cm3
Volume of hemisphere = (⅔)×π×103 cm3
Volume of cylinder = π×602×180 = 648000 = 648×103 π cm3
Now, volume of water left will be = Volume of cylinder – Volume of solid
= (648-288) × 103×π = 1.131 m3
8. A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.
Solution:
Given,
For the cylinder part, Height (h) = 8 cm and Radius (R) = (2/2) cm = 1 cm
For the spherical part, Radius (r) = (8.5/2) = 4.25 cm

Now, volume of this vessel = Volume of cylinder + Volume of sphere
= π×(1)2×8+(4/3)π(1)3
= 346.51 cm3
Exercise: 13.3
(Page No: 251)
1. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution:
It is given that radius of the sphere (R) = 4.2 cm
Also, Radius of cylinder (r) = 6 cm
Now, let height of cylinder = h
It is given that the sphere is melted into a cylinder.
So, Volume of Sphere = Volume of Cylinder
∴ (4/3)×π×R3 = π×r2×h.
h = 2.74 cm
2. Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Solution:
For Sphere 1:
Radius (r1) = 6 cm
∴ Volume (V1) = (4/3)×π×r13
For Sphere 2:
Radius (r2) = 8 cm
∴ Volume (V2) = (4/3)×π×r23
For Sphere 3:
Radius (r3) = 10 cm
∴ Volume (V3) = (4/3)× π× r33
Also, let the radius of the resulting sphere be “r”
Now,
Volume of resulting sphere = V1+V2+V3
(4/3)×π×r3 = (4/3)×π×r13+(4/3)×π×r23 +(4/3)×π×r33
r3 = 63+83+103
r3 = 1728
r = 12 cm
3. A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution:
It is given that the shape of the well is in the shape of a cylinder with a diameter of 7 m
So, radius = 7/2 m
Also, Depth (h) = 20 m
Volume of the earth dug out will be equal to the volume of the cylinder
∴ Volume of Cylinder = π×r2×h
= 22×7×5 m3
Let the height of the platform = H
Volume of soil from well (cylinder) = Volume of soil used to make such platform
π×r2×h = Area of platform × Height of the platform
We know that the dimension of the platform is = 22×14
So, Area of platform = 22×14 m2
∴ π×r2×h = 22×14×H
⇒ H = 2.5 m
4. A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Solution:
The shape of the well will be cylindrical as given below.

Given, Depth (h1) of well = 14 m
Diameter of the circular end of the well =3 m
So, Radius (r1) = 3/2 m
Width of the embankment = 4 m
From the figure, it can be said that the embankment will be a cylinder having an outer radius (r2) as 4+(3/2) = 11/2 m and inner radius (r1) as 3/2m
Now, let the height of embankment be h2
∴ Volume of soil dug from well = Volume of earth used to form embankment
π×r12×h = π×(r22-r12) × h2
Solving this, we get,
The height of the embankment (h2) as 1.125 m.
5. A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Solution:
Number of cones will be = Volume of cylinder / Volume of ice cream cone
For the cylinder part,
Radius = 12/2 = 6 cm
Height = 15 cm
∴ Volume of cylinder = π×r2×h = 540π
For the ice cone part,
Radius of conical part = 6/2 = 3 cm
Height = 12 cm
Radius of hemispherical part = 6/2 = 3 cm
Now,
Volume of ice cream cone = Volume of conical part + Volume of hemispherical part
= (⅓)×π×r2×h+(⅔)×π×r3
= 36π +18π
= 54π
∴ Number of cones = (540π/54π)
= 10
6. How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?
Solution:
It is known that the coins are cylindrical in shape.
So, height (h1) of the cylinder = 2 mm = 0.2 cm
Radius (r) of circular end of coins = 1.75/2 = 0.875 cm
Now, the number of coins to be melted to form the required cuboids be “n”
So, Volume of n coins = Volume of cuboids
n × π × r2 × h1 = l × b × h
n×π×(0.875)2×0.2 = 5.5×10×3.5
Or, n = 400
7. A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution:
The diagram will be as-

Given,
Height (h1) of cylindrical part of the bucket = 32 cm
Radius (r1) of circular end of the bucket = 18 cm
Height of the conical heap ((h2) = 24 cm
Now, let “r2” be the radius of the circular end of the conical heap.
We know that volume of the sand in the cylindrical bucket will be equal to the volume of sand in the conical heap.
∴ Volume of sand in the cylindrical bucket = Volume of sand in conical heap
π×r12×h1 = (⅓)×π×r22×h2
π×182×32 = (⅓)×π ×r22×24
Or, r2= 36 cm
And,
Slant height (l) = √(362+242) = 12√13 cm.
8. Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Solution:
It is given that the canal is the shape of a cuboid with dimensions as:
Breadth (b) = 6 m and Height (h) = 1.5 m
It is also given that
The speed of canal = 10 km/hr
Length of canal covered in 1 hour = 10 km
Length of canal covered in 60 minutes = 10 km
Length of canal covered in 1 min = (1/60)x10 km
Length of canal covered in 30 min (l) = (30/60)x10 = 5km = 5000 m
We know that the canal is cuboidal in shape. So,
Volume of canal = lxbxh
= 5000x6x1.5 m3
= 45000 m3
Now,
Volume of water in canal = Volume of area irrigated
= Area irrigated x Height
So, Area irrigated = 56.25 hectares
∴ Volume of canal = lxbxh
45000 = Area irrigatedx8 cm
45000 = Area irrigated x (8/100)m
Or, Area irrigated = 562500 m2 = 56.25 hectares.
9. A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Solution:
Consider the following diagram-


Volume of water that flows in t minutes from pipe = t×0.5π m3
Volume of water that flows in t minutes from pipe = t×0.5π m3
Radius (r2) of circular end of cylindrical tank =10/2 = 5 m
Depth (h2) of cylindrical tank = 2 m
Let the tank be filled completely in t minutes.
Volume of water filled in tank in t minutes is equal to the volume of water flowed in t minutes from the pipe.
Volume of water that flows in t minutes from pipe = Volume of water in tank
t×0.5π = π×r22×h2
Or, t = 100 minutes
Exercise: 13.4 (Page No: 257)
1. A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:
Radius (r1) of the upper base = 4/2 = 2 cm
Radius (r2) of lower the base = 2/2 = 1 cm
Height = 14 cm
Now, Capacity of glass = Volume of frustum of cone
So, Capacity of glass = (⅓)×π×h(r12+r22+r1r2)
= (⅓)×π×(14)(22+12+ (2)(1))
∴ The capacity of the glass = 102×(⅔) cm3
2. The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the surface area of the frustum.
Solution:
Given,
Slant height (l) = 4 cm
Circumference of upper circular end of the frustum = 18 cm
∴ 2πr1 = 18
Or, r1 = 9/π
Similarly, circumference of lower end of the frustum = 6 cm
∴ 2πr2 = 6
Or, r2 = 6/π
Now, CSA of frustum = π(r1+r2) × l
= π(9/π+6/π) × 4
= 12×4 = 48 cm2
3. A fez, the cap used by the Turks, is shaped like the frustum of a cone (see Fig.). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.

Solution:
Given,
For the lower circular end, radius (r1) = 10 cm
For the upper circular end, radius (r2) = 4 cm
Slant height (l) of frustum = 15 cm
Now,
The area of material to be used for making the fez = CSA of frustum + Area of upper circular end
CSA of frustum = π(r1+r2)×l
= 210π
And, Area of upper circular end = πr22
= 16π
∴ The area of material used = 710 × (2/7) cm2
4. A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of Rs. 20 per litre. Also find the cost of metal sheet used to make the container, if it costs Rs. 8 per 100 cm2.
Solution:
Given,
r1 = 20 cm,
r2 = 8 cm and
h = 16 cm
∴ Volume of the frustum = (⅓)×π×h(r12+r22+r1r2)

It is given that the rate of milk = Rs. 20/litre
So, Cost of milk = 20×volume of the frustum

= Rs. 209
Now, slant height will be

So, CSA of the container = π(r1+r2)×l

= 1758.4 cm2
Hence, the total metal that would be required to make container will be = 1758.4 + (Area of bottom circle)
= 1758.4+201 = 1959.4 cm2
∴ Total cost of metal = Rs. (8/100) × 1959.4 = Rs. 157
5. A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire.
Solution:
The diagram will be as follows

Consider AEG

Radius (r1) of upper end of frustum = (10√3)/3 cm
Radius (r2) of lower end of container = (20√3)/3 cm
Height (r3) of container = 10 cm
Now,
Volume of the frustum = (⅓)×π×h(r12+r22+r1r2)

Solving this we get,
Volume of the frustum = 22000/9 cm3
The radius (r) of wire = (1/16)×(½) = 1/32 cm
Now,
Let the length of wire be “l”.
Volume of wire = Area of cross-section x Length
= (πr2)xl
= π(1/32)2x l
Now, Volume of frustum = Volume of wire
22000/9 = (22/7)x(1/32)2x l
Solving this we get,
l = 7964.44 m
Exercise: 13.5 (Optional) (Page No: 258)
1. A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
Solution:
Given that,
Diameter of cylinder = 10 cm
So, radius of the cylinder (r) = 10/2 cm = 5 cm
∴ Length of wire in completely one round = 2πr = 3.14×5 cm = 31.4 cm
It is given that diameter of wire = 3 mm = 3/10 cm
∴ The thickness of cylinder covered in one round = 3/10 m
Hence, the number of turns (rounds) of the wire to cover 12 cm will be-

Now, the length of wire required to cover the whole surface = length of wire required to complete 40 rounds
40 x 31.4 cm = 1256 cm
Radius of the wire = 0.3/2 = 0.15 cm
Volume of wire = Area of cross-section of wire × Length of wire
= π(0.15)2×1257.14
= 88.898 cm3
We know,
Mass = Volume × Density
= 88.898×8.88
= 789.41 gm
2. A right triangle whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate)
Solution:
Draw the diagram as follows:

Let us consider the ABA
Here,
AS = 3 cm, AC = 4 cm
So, Hypotenuse BC = 5 cm
We have got 2 cones on the same base AA’ where the radius = DA or DA’
Now, AD/CA = AB/CB
By putting the value of CA, AB and CB we get,
AD = 2/5 cm
We also know,
DB/AB = AB/CB
So, DB = 9/5 cm
As, CD = BC-DB,
CD = 16/5 cm
Now, volume of double cone will be

Solving this we get,
V = 30.14 cm3
The surface area of the double cone will be

= 52.75 cm2
3. A cistern, internally measuring 150 cm × 120 cm × 100 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each being 22.5 cm × 7.5 cm × 6.5 cm?
Solution:
Given that the dimension of the cistern = 150 × 120 × 110
So, volume = 1980000 cm3
Volume to be filled in cistern = 1980000 – 129600
= 1850400 cm3
Now, let the number of bricks placed be “n”
So, volume of n bricks will be = n×22.5×7.5×6.5
Now as each brick absorbs one-seventeenth of its volume, the volume will be
= n/(17)×(22.5×7.5×6.5)
For the condition given in the question,
The volume of n bricks has to be equal to volume absorbed by n bricks + Volume to be filled in cistern
Or, n×22.5×7.5×6.5 = 1850400+n/(17)×(22.5×7.5×6.5)
Solving this we get,
n = 1792.41
4. In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 97280 km2, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
Solution:
From the question, it is clear that
Total volume of 3 rivers = 3×[(Surface area of a river)×Depth]
Given,
Surface area of a river = [1072×(75/1000)] km
And,
Depth = (3/1000) km
Now, volume of 3 rivers = 3×[1072×(75/1000)]×(3/1000)
= 0.72 km3
Now, volume of rainfall = total surface area × total height of rain

= 9.7 km3
For the total rainfall was approximately equivalent to the addition to the normal water of three rivers, the volume of rainfall has to be equal to volume of 3 rivers.
But, 9.7 km3 ≠ 0.72 km3
So, the question statement is false.
5. An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see Fig.).

Solution:
Given,
Diameter of upper circular end of frustum part = 18 cm
So, radius (r1) = 9 cm
Now, the radius of the lower circular end of frustum (r2) will be equal to the radius of the circular end of the cylinder
So, r2 = 8/2 = 4 cm
Now, height (h1) of the frustum section = 22 – 10 = 12 cm
And,
Height (h2) of cylindrical section = 10 cm (given)
Now, the slant height will be-

Or, l = 13 cm
Area of tin sheet required = CSA of frustum part + CSA of cylindrical part
= π(r1+r2)l+2πr2h2
Solving this we get,
Area of tin sheet required = 782×(4/7) cm2
6. Derive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
Solution:
Consider the diagram

Let ABC be a cone. From the cone the frustum DECB is cut by a plane parallel to its base. Here, r1 and r2 are the radii of the frustum ends of the cone and h be the frustum height.
Now, consider the ΔABG and ΔADF,
Here, DF||BG
So, ΔABG ~ ΔADF

Now, by rearranging we get,

The total surface area of frustum will be equal to the total CSA of frustum + the area of upper circular end + area of the lower circular end
= π(r1+r2)l+πr22+πr12
∴ Surface area of frustum = π[r1+r2)l+r12+r22]
7. Derive the formula for the volume of the frustum of a cone.
Solution:
Consider the same diagram as the previous question.

Now, approach the question in the same way as the previous one and prove that
ΔABG ~ ΔADF
Again,

Now, rearrange them in terms of h and h1

The total volume of frustum of the cone will be = Volume of cone ABC – Volume of cone ADE
= (⅓)πr12h1 -(⅓)πr22(h1 – h)
= (π/3)[r12h1-r22(h1 – h)]

Now, solving this we get,
∴ Volume of frustum of the cone = (⅓)πh(r12+r22+r1r2)

Comments
Post a Comment